布隆(bloom)过滤器
布隆过滤器用于高效检索一个元素是否在一个集合中,空间效率和查询时间比一般的算法都要好。根据其定义,布隆过滤器可以检查值是“可能在集合中”还是“绝对不在集合中”。“可能”表示有一定的概率,也就是说可能存在一定的误判率。
Guava布隆过滤器演示
- 1、引入依赖
pom.xml
<properties>
<maven.compiler.source>8</maven.compiler.source>
<maven.compiler.target>8</maven.compiler.target>
</properties>
<dependencies>
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>22.0</version>
</dependency>
<dependency>
<groupId>junit</groupId>
<artifactId>junit</artifactId>
<version>4.13.2</version>
<scope>test</scope>
</dependency>
</dependencies>
- 2、编写测试类
AppTest.java
import com.google.common.base.Charsets;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
import org.junit.Test;
import static org.junit.Assert.*;
public class AppTest {
@Test
public void test() {
int total = 5_000_000;
BloomFilter<CharSequence> bloom = BloomFilter.create(Funnels.stringFunnel(Charsets.UTF_8), total);
for (int i = 0; i < total; i++) {
bloom.put(String.valueOf(i * 2));
}
assertTrue(bloom.mightContain(String.valueOf(2)));
assertTrue(bloom.mightContain(String.valueOf(4)));
assertTrue(bloom.mightContain(String.valueOf(6)));
assertTrue(bloom.mightContain(String.valueOf(8_888_888)));
}
}
初始化布隆过滤器的时候,需要传入期望处理的元素数量,以及期望的误报率(默认误报率是0.03)。
在模拟测试中将500万个偶数初始化到bloom过滤器中,同时判断500万个奇数是否在bloom过滤器中,观察误报率的情况;
int error = 0;
for (int i = 0; i < total; i++) {
if (bloom.mightContain(String.valueOf(i * 2 + 1))) {
error++;
}
}
System.out.println("误报总数为 " + error);
结论:误报总数为 149130,计算的确是约为3%误报,将误报率改为0.0003,BloomFilter.create(Funnels.stringFunnel(Charsets.UTF_8), total,0.0003);,再次运行查看结果,其误报总数为 1486;
- 3、查看误报是怎么产生的?
回到代码跟踪看一下误报率为默认的0.03时,误报是怎么产生的,通过以下代码找到第一个误报的奇数
for (int i = 0; i < total; i++) {
if (bloom.mightContain(String.valueOf(i * 2 + 1))) {
System.out.println("第一个误报的数据为"+(i * 2 + 1));
break;
}
}
结果第一个误报的数据为91,91为奇数,显然不应该在过滤器中,看一下源码的计算方式。
查看BloomFilter的源码,可以看到默认的误报率默认是0.03,计算的hash函数的个数为5个
public static <T> BloomFilter<T> create(Funnel<? super T> funnel, long expectedInsertions) {
return create(funnel, expectedInsertions, 0.03); // FYI, for 3%, we always get 5 hash functions
}
...
long numBits = optimalNumOfBits(expectedInsertions, fpp);
int numHashFunctions = optimalNumOfHashFunctions(expectedInsertions, numBits);
...
查看mightContain方法,可以看到在此例子中,由5个hash函数判断,若均命中,则判断为可能存在,若一个不命中(印证“绝对不在集合中”)则在循环中直接返回false了,表示不存在,如下
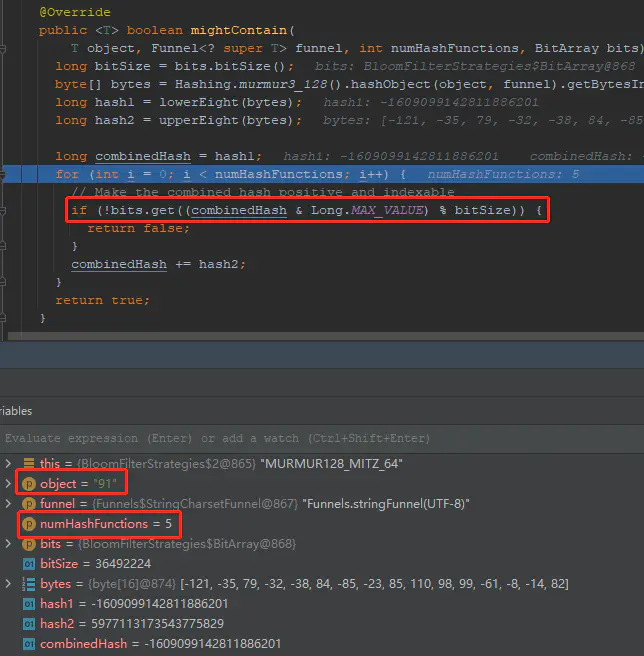
记录一下i从0~4时值情况,其中位置值是通过(combinedHash & Long.MAX_VALUE) % bitSize计算得出,出现了误报说明某一位置已有值了,记录表如下
| i的值 | combineHash值 | bitSize值 | 位置值 |
|---|---|---|---|
| 0 | -1609099142811886201 | 36492224 | 12543751 |
| 1 | 4368014030731889628 | 36492224 | 16508188 |
| 2 | -8101616869433886159 | 36492224 | 20472625 |
| 3 | -2124503695890110330 | 36492224 | 24104710 |
| 4 | 3852609477653665499 | 36492224 | 28069147 |
接着反过来模拟,在初始化bloom过滤器的时候改造一下进行判断跟踪,找出第一个加入bloom过滤器时引起91产生误报的数,代码如下
for (int i = 0; i < total; i++) {
bloom.put(String.valueOf(i * 2));
if(bloom.mightContain("91")){
System.out.println("出现误报,初始化终止,当前数据为"+(i*2));
System.exit(1);
}
}
结果为:出现误报,初始化终止,当前数据为6677518,即当i=3338759时出现了误报,跟踪调试进入bloom.put方法,源码关键部分如下
public <T> boolean put(
T object, Funnel<? super T> funnel, int numHashFunctions, BitArray bits) {
...
for (int i = 0; i < numHashFunctions; i++) {
// Make the combined hash positive and indexable
bitsChanged |= bits.set((combinedHash & Long.MAX_VALUE) % bitSize);
combinedHash += hash2;
}
return bitsChanged;
}
调试阶段,同样获取一份记录表,记录i从0~4的时候,bits.set操作的位置信息,如下
| i的值 | combineHash值 | bitSize值 | 位置值 |
|---|---|---|---|
| 0 | 5014738958618502248 | 36492224 | 20337704 |
| 1 | 8022776140390556657 | 36492224 | 20472625 |
| 2 | -7415930751546940550 | 36492224 | 20939898 |
| 3 | -4407893569774886141 | 36492224 | 21074819 |
| 4 | -1399856388002831732 | 36492224 | 21209740 |
结论:可以看到位置20472625冲突了,导致了误报,即以下两个打印值相等
System.out.println((8022776140390556657L & Long.MAX_VALUE) % 36492224);
System.out.println((-8101616869433886159L & Long.MAX_VALUE) % 36492224);
